Dernières nouvelles de l'homme

Une journée à l’assemblée nationale.

Invités par notre député, Claude Birraux, nous (une dizaine d'élus locaux) avons pris le TGV puis le métro jusqu’à la Madeleine. Nous sommes donc arrivés au palais Bourbon par la rue Royale, la place de la Concorde puis le pont avec un vent glacial mais un ciel tout bleu et un beau coup d'oeil sur Paris.

Le matin, visite de l’assemblée, la salle des pas perdus, la salle des quatre colonnes, l’hémicycle… Ensuite, repas offert par le député dans un petit salon fort sympathique. Menu gastronomique, discussion sur le job de député et en particulier celui de président de l’OPECST, l’office parlementaire d'évaluation des choix scientifiques et technologiques. On parle aussi des gazs de schiste suite à la question posée à NKM, la semaine précédente et  dont la réponse n’a pas eut l'heur de plaire à Claude.

A trois heures, la session des questions au gouvernement. Un grand nombre de ministres autour du premier, Guéant content de lui, Morano qu’a même pas dit une seule ânerie, Juppé, Chatel, Pécresse, Baroin, Apparu, NKM, Mitterand… Le président reparle de l’incident du jour précédent (Serge Letchimy s’en prenant à Guéant) et on attaque les questions. Pas terribles. Celles de la majorité sont convenues, les réponses aussi. Parmi celles de l’opposition, à noter Philippe Plisson, un girondin de Gironde. Voir ci-dessous.

Puis visite du rez de chaussée de l’hôtel de Lassay séparé du palais Bourbon par une magnifique salle. Ici, ce sont les ors de la république. Trois fleuristes à temps plein. Greg adore… c’est son côté monarchie british. Ensuite on se rend à la résidence Chaban-Delmas, le bureau de Claude Birraux, immeuble moderne mais pas de luxe excessif.

Claude doit partir mais il a laissé pour moi un petit fascicule, rapport sur LES MATHÉMATIQUES EN FRANCE ET DANS LES SCIENCES  en présence des lauréats de la médaille Fields,  MM. Ngô Bảo Châu et Cédric Villani,  ainsi que du lauréat du prix Gauss, M. Yves Meyer (photo). Trois génies des mathématiques. Une attention qui me touche. La journée est finie, retour sur St Julien.

Question de Philippe Plisson :

Ma question s’adresse à Mme la ministre du budget et des comptes publics, qui s’est apparemment éclipsée pour ne pas avoir à répondre à ma question embarrassante. (Pécresse est partie) La proposition du président-candidat d’augmenter de 30 % les surfaces constructibles recueille une belle unanimité, y compris du président de la chambre des notaires, pour dire qu’elle ne servira à rien sinon à augmenter considérablement le prix des terrains.

À ce propos, Mme la ministre a péremptoirement affirmé sur France Inter, mardi dernier, que la mesure va à tout coup infléchir à la baisse les prix de l’immobilier. Quand le journaliste lui a répondu que les constructions neuves seraient dorénavant taxées non plus à 19,6 % mais à 21,2 %, elle a rétorqué, je la cite : « Dans la construction, la TVA est à 7 %. » (Rires sur plusieurs bancs du groupe SRC.)

Cette allégation est fausse, comme l’atteste le site officiel de son ministère, impots.gouv.fr, qui indique que « le taux de TVA réduite est exclu pour les travaux qui concourent par leur nature ou leur ampleur à la production d’un immeuble neuf ».(Applaudissements sur les bancs des groupes SRC et GDR.)

Placée devant la contradiction, elle persiste dans l’erreur : « Si un particulier décide de faire agrandir son logement de 30 %, il fera des travaux de rénovation et paiera donc la TVA à 7 %. » (« Oh ! » sur les bancs des groupes SRC et GDR.) Il s’agit à nouveau d’une affirmation fausse puisque l’instruction fiscale à ce sujet est limpide : « Le taux à 7 % ne porte pas sur les travaux qui conduisent à une surélévation du bâtiment ou à une addition de construction. »

Dans tous les cas, contrairement à ce que la ministre a martelé, ces travaux de construction seront bien taxés au taux de votre nouvelle TVA antisociale, 21,2 %.

Alors ma question est simple : la ministre méconnaît-elle les règlements de son ministère ou ment-elle délibérément aux Français ?

Réponse à côté de la plaque de Benoist Apparu.

Dessine-moi un poisson.

Comme chacun sait, le poisson est l’animal le plus facile à dessiner depuis que Findus en a fait un animal parallélépipédique (pas facile à écrire par contre).

Les poissons vont disparaître, c’est ce que nous dit Findus qui ne peut bientôt plus utiliser de merlan bleu pour le surimi, ni le merlu du Pacifique pour les tranches panées.

Soyez rassurés braves gens, Findus a connu une croissance de 7% en 2011. Quand les parallélépipèdes ne contiendront plus que de la panure enveloppant des molécules chimiques et quelques traces de poisson vendues à prix d’or, Findus continuera d’engraisser ses bénéfices et de dégraisser son personnel et le Figaro de vous parler de la raréfaction du poisson 

Mais tous les poissons sont-ils égaux ? Non, bien sûr, il y a en a de plus égaux que d'autres. D’un côté, les prédateurs (carnivores) et de l’autre les proies (herbivores) et quelques espèces carnivores au milieu mais qui se font fait bouffer par des plus gros qu'elles. Pour simplifier, Alfred James Lotka en 1925 et Vito Volterra en 1926 ont pris les proies et les prédateurs et ont posé, chacun de leur côté, des équations qui expliquent la croissance des deux populations. Voir sur Wiki.

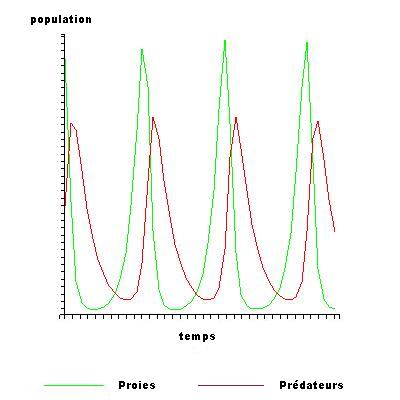
Les équations admettent des solutions périodiques qui n'ont pas d'expression simple à l'aide des fonctions trigonométriques habituelles. Néanmoins, une solution approximative linéarisée offre un mouvement harmonique simple, avec la population des prédateurs en retard de 90° (un quart de période) sur celle des proies. Voir schéma. Dans le modèle utilisé, les prédateurs prospèrent lorsque les proies sont nombreuses, mais finissent par épuiser leurs ressources et déclinent lorsque la population de prédateur a suffisamment diminué, les proies profitant du répit se reproduisent et leur population augmente de nouveau. Cette dynamique se poursuit en un cycle de croissance et déclin.

A noter que ces équations marchent aussi pour le lynx et le lièvre des neiges, pour le lion et la gazelle, le cachalot et le phoque… Par contre elles ne disent pas ce qui se passe quand le prédateur marche sur deux pattes en utilisant son gros cerveau pour compter les billets de banque. Mais, dans ce cas, on peut prévoir que les deux courbes finiront par faire plouf dans l’eau et la vie sur terre avec.

A noter encore que les mêmes équations, magie des mathématiques, ont été utilisées par Allan Hobson, neuropsychiatre américain, pour décrire les relations entre les neurones cholinergiques responsables du sommeil paradoxal et les neurones aminergiques liées à l'état de veille. Il a fait L'hypothèse de l'activation-synthèse (AS) en posant que les rêves sont issus de l'activation aléatoire des neurones dans le cortex cérébral. Le cerveau fait de son mieux pour attribuer un sens aux signaux, dans les conditions de travail défavorables du sommeil paradoxal. Cette hypothèse basée sur un modèle mathématique, se présente comme une critique des thèses psychanalytiques.

Allan (photo) a 79 ans et le sourire.

Connaissez-vous les sphères cornues ?

Savez-vous ce qu’est un espace connexe ?

La France n’est pas connexe, L’Espagne non plus. Par contre la France métropolitaine sans la Corse et les enclaves est connexe et ce que les espagnols appellent La Peninsula est aussi connexe à condition de ne pas considérer les Baléares comme partie de la Peninsula... En topologie, un espace connexe est donc un espace d’un seul tenant. Facile !

Le mathématicien lyonnais Camille Jordan (1838-1922) tenait absolument à démontrer qu’un lacet posé sur un plan partageait l’espace en deux parties. En effet, contrairement à Kant qui pensait que les mathématiques sont fondées sur l'évidence intuitive des choses, Jordan croit en la démonstration à tout prix... et donc...

Il démontre très difficilement et plus ou moins bien le coup du lacet. Notamment, il explique qu’une droite (verte) tracée d’un point à l’intérieur du lacet (bleu) le coupe un nombre impair de fois, et une droite (rouge) tracées d'un point extérieur le coupe un nombre pair de fois.

D’autre feront d’autres démonstrations et bien sûr tenteront d’étendre le problème aux dimensions supérieur à 2. C’est une manie chez les mathématiciens de tenter des généralisations. Mais en réfléchissant aux surfaces fermées de l’espace*, Alexander a découvert en 1923 qu’il existait une drôle de bestiole qui ne se laissait pas enlacer même avec le meilleur lacet ou lassot. C’est la sphère cornue d’Alexander. Une fractale. Voilà comment on la construit... Photo et video.

La sphère cornue est appelé une surface pathologique. En mathématiques, un objet pathologique désigne un objet qui s'oppose à l'intuition que l'on a de la situation générale. Un peu malade quand même.

Je vous laisse méditer la phrase de Poincaré :

« La logique parfois engendre des monstres. On vit surgir toute une foule de fonctions bizarres qui semblaient s'efforcer de ressembler aussi peu que possible aux honnêtes fonctions qui servent à quelque chose. Plus de continuité, ou bien de la continuité, mais pas de dérivées [...] Autrefois, quand on inventait une fonction nouvelle, c'était en vue de quelque but pratique ; aujourd'hui, on les invente tout exprès pour mettre en défaut les raisonnements de nos pères, et on n'en tirera jamais que cela. »

* Quel est le nombre de dimensions d’une surface fermée de l’espace, surface fractale, comme la sphère cornue, 2 ou 3 ?

On peut penser que la réponse est 2, virgule des bricoles. Les fractales définissent des espaces à dimensions non entières. Les matheux comprendront pourquoi.

Les statisticiens  nous ont fait croire que un million de singes frappant sur un million de machines à écrire produiraient tôt ou tard une histoire qui tienne debout. Maintenant, grâce à l’internet, nous savons que ce n'est pas vrai.

La démonstration est faite car on a largement dépassé le million d’internautes tapant sur un million de claviers et on n’a toujours pas eu le premier mot de cette histoire. Il faut donc une sacrée dose d’optimisme pour croire que cela viendra un jour.

D’ailleurs, en probabilités, la loi du zéro un de Kolmogorov affirme que certains événements, appelés événements queues (queues de singes bien sûr), soit seront presque sûrement réalisés, soit ne seront presque sûrement pas réalisés. Le zéro est ici évident.

Ceci est la 1500^ième  note de ce blog crée pour ajouter quelques caractères au bruit des 1499 autres.

Les mathématiciens adorent utiliser un mot courant pour désigner un truc éminemment abstrait mais très très bien défini. C’est le cas des corps, des anneaux, des idéaux. Les nombres sont entiers, réels, imaginaires, complexes et idéaux eux aussi. Bourbaki a ainsi nommé les boules, les pavés (sous les pavés, la plage), les filtres, le recouvrement, le revêtement, les espaces séparés, les tonneaux, les espaces tonnelés, les espaces polonais, les clans, les tribus…

Une boule topologique n'a qu'un lointain rapport avec une sphère.

En effet, Dans l'espace réel à trois dimensions muni de la norme infini, les boules ont une forme cubique avec des faces parallèles aux axes.

Ou encore, dans un espace muni d'une distance ultramétrique, les boules sont à la fois ouvertes et fermées, tout point d'une boule en est un centre et si deux boules se rencontrent, l'une est contenue dans l'autre. De tels espaces se rencontrent en analyse p-adique mais aussi dans des situations plus élémentaires. Quelle chance !

En cherchant p-adique, on tombe sur un mathématicien français d'origine belge et encore vivant du nom de Tits. Tits qui signifie seins en anglais. Drôle de nom pour un spécialiste des boules ! Jacques Tits est né en 1930. Il est en fait le spécialiste des BN-paires (pas les chocos), très utiles dans la théorie des groupes algébriques surtout pour les groupes définis sur les nombres p-adiques. Bien sûr, les boules !

Tits a créé des mots lui aussi. Il inventa les notions importantes de squelette, de cimetière, et d'ossuaire. Les mathématiciens sérieux, les censeurs, les ont rebaptisé murs, appartements et immeubles... Franchement pourquoi pas des briques et du mortier tant qu’on y est. C'est un scandale. On veut décourager les jeunes gothiques de s’intéresser aux maths !

Les habitants de l'île de Délos souffraient de la peste. Délos est une île grecque des Cyclades de 3,5 km2, aujourd’hui inhabitée ou l’on peut voir les restes d’un temple à Apollon. L’île  aurait compté 25'000 habitants. L'oracle recommanda de purifier l’île et de doubler le volume de l’autel dédié à Apollon.

Pour la purification, très simple, on interdit de naître et de mourir sur l’île. Pour l’autel, problème… l’autel était exactement cubique. De nombreuses tentatives échouaierent. La peste redoublait. Alors, les déliens allèrent chercher les conseils de Platon. Platon sécha… finalement, il prétendit qu’Apollon n'avait pas besoin d'un nouvel autel et que les déliens feraient bien de s’intéresser de près à la géométrie.

Le doublement du cube est un des trois problèmes de l’antiquité avec la quadrature du cercle, la trisection de l’angle. Il est impossible de trouver racine cubique de 2 avec une règle et un compas. Démonstration faite en 1837 par un mathématicien français Pierre-Laurent Wantzel. On ne vantera jamais assez l’école française de mathématique. A noter que l’on peut résoudre le problème du doublement du cube et de la trisection par pliage de papier. Ah, si Platon avait connu l’origami.

La cicadelle (Homalodisca vitripennis ou encore coagulata) improprement appelée  mouche pisseuse est proche des cigales. Elle mesure entre 1,5 et 2 cm. On l’appelle pisseuse car elle suce la sève des arbres, séve peut nourissante et dont elle rejette cent à mille fois son propre poids chaque jour ce qui provoque une fine pluie légèrement sirupeuse à l'ombre des arbres.

Cette bestiole, originaire du sud des États-Unis, où elle ne pose pas de problème, s'est propagée en Californie (1988), en Polynésie française(1999), à Hawaii 2004 et à l'île de Pâques 2005, où elle est considérée comme une espèce invasive. Elle est susceptible de transmettre des maladies aux plantes.

Une méthode de lutte biologique contre la cicadelle pisseuse consiste à installer une petite guêpe qui pond ses œufs dans les larves de cicadelle. Ceci réduit notablement le nombre de cicadelles.

Mais les mathématiciens font mieux, ils simulent la vie et la reproduction de la cicadelle pisseuse. Celle-ci vit en symbiose avec deux bactéries (ses symbions). Bactéries qui ont aussi des échanges entre elles pour survivre. En simulant ainsi la vie des mouches pisseuses et de ses hôtes, les maths vont peut-être permettre de trouver une manière de limiter sa prolifération. On pourrait peut-être supprimer une de ces bactéries symbiotes qui aide la cicadelle à synthétiser certaines protéines… mais là, je m’avance un peu.

Symbiose : de sun> avec et bio> la vie. Association entre deux organismes. Une sorte de parasitisme dans l'intérêt des deux (ou plus, voir cicadelle pisseuse).  Symbion - Un des deux alliés. Symbiote : adj > qui vit en symbiose