Dernières nouvelles de l'homme

En 2019 j’avais commis une note très sérieuse sur Emmy Noether.

Et aujourd’hui je retombe sur cette dame d’une intelligence plus qu’exceptionnelle. Elle a rencontré pas mal d’obstacles dus à son genre. En 1915, le grand mathématicien David Hilbert l’invite à Göttingen. Un membre de la faculté proteste :

"Que penseront nos soldats, quand ils reviendront à l'université et verront qu'ils doivent apprendre aux pieds d'une femme ?" Hilbert répond avec indignation : « je ne vois pas pourquoi le sexe de la candidate serait un argument contre son admission comme Privatdozent. Après tout, nous sommes une université, pas des bains publics. »

Bon, assez de sérieux. Pour suivre Noether, cent ans plus tard, il faut encore faire parti des tout tout forts en math. Mais on peut s’intéresser à la poésie des maths.

Wikipedia : « Au cours de la deuxième époque (1920-1926), elle commence des travaux "qui ont changé la face de l'algèbre". Dans son article devenu un classique,  Noether développe la théorie des idéaux dans les anneaux commutatifs… Elle fait un usage élégant de la condition de chaîne ascendante, et les objets qui satisfont à cette condition sont dits noethériens en son honneur. Pendant sa troisième époque (1927-1935), elle publie des avancées majeures en algèbre non commutative et sur les nombres hypercomplexes, et unit la théorie des représentations de groupes avec celle des modules et des idéaux.

Groupes, modules, idéaux, anneaux... C'est beau.     

Bon d'accord, mais c’est quoi des hypercomplexes ?

Le terme nombre hypercomplexe est utilisé pour désigner des nombres qui vont plus loin que l'arithmétique des nombres complexes.

On s'en doutait !

Les complexes de base (C) sont des nombres en 2D,

en 4D on a les quaternions H,

en 8 les Octonions,

en 16 les Sedognions,

en 32 les Parthion...

Pas encore de noms pour les oignions 512, 1024, 2048, 4096... A vous de jouer. 

Emmy Noether (1882 – 1935) naît dans une famille juive d'Erlangen en Bavière. Son père est le mathématicien Max Noether. Emmy envisage d'abord d'enseigner le français et l'anglais après avoir passé les examens requis, mais étudie finalement les mathématiques à l'université d'Erlangen où son père donne des conférences.

Elle achève sa thèse en 1907 et travaille bénévolement à l'Institut de Mathématiques d'Erlangen pendant sept ans. En 1915, elle est invitée par David Hilbert et Felix Klein (excusez du peu) à rejoindre le très renommé département de mathématiques de l'université de Göttingen. Mais la faculté de philosophie refuse qu'une femme soit nommée professeur. Pendant quatre ans elle donne des cours sous le nom de Hilbert. Son habilitation est obtenue en 1919.

Pour ses travaux en physique, elle aurait dû figurer avec Marie Curie sur la fameuse photo de classe du congrès de Solvay en 1927 et ses 17 prix Nobel. Mais elle était sans doute trop modeste, on ne l'a pas invitée.

Albert Einstein dira d’elle qu'elle était « le génie mathématique créatif le plus considérable produit depuis que les femmes ont eu accès aux études supérieures ». En fait elle était un génie au delà de son genre, toute catégories confondues. Elle va révolutionner les théories des anneaux, des corps et des algèbres. En physique, le théorème de Noether explique le lien fondamental entre la symétrie et les lois de conservation et est considéré comme aussi important que la théorie de la relativité.

Emmy Noether est alors  un des membres les plus influents du département de mathématiques de Göttingen jusqu'en 1933. Avant même son intervention au congrès international des mathématiciens de Zurich (1932), sa connaissance de l'algèbre est reconnue dans le monde entier. L'année suivante, le gouvernement nazi exclut les Juifs qui occupent des postes universitaires et Noether émigre alors aux États-Unis où elle obtient un poste au Bryn Mawr College et mourra bientôt.

Bien que le théorème de Noether ait un profond effet sur la physique, elle est plus connue parmi les mathématiciens pour ses contributions fondatrices en algèbre générale. Nathan Jacobson (1910-1999) affirme :

« Le développement de l'algèbre abstraite, qui est l'une des innovations les plus caractéristiques des mathématiques du vingtième siècle, lui est largement redevable, par les articles qu'elle a publiés, par ses conférences et son influence personnelle sur ses contemporains. »

Ses collègues diront que ses travaux étaient révolutionnaires que l'originalité de Noether était absolue, au-delà de toute comparaison. Emmy ne recherche pas la reconnaissance. Elle laisse parfois à ses collègues et étudiants le crédit pour ses propres idées, les aidant ainsi à développer leur carrière à ses dépens.

Ceux qui vivaient dans les années soixante et septante, 60 et 70 donc, se souviennent de la réforme des maths dite des maths modernes. En fait ce modernisme datait du début du siècle. Et même en ce qui concerne les précurseurs du début du siècle d’avant. Ils s’appelaient du Evariste Galois (1819-1832) et Niels Henrik Abel (1802-1829).

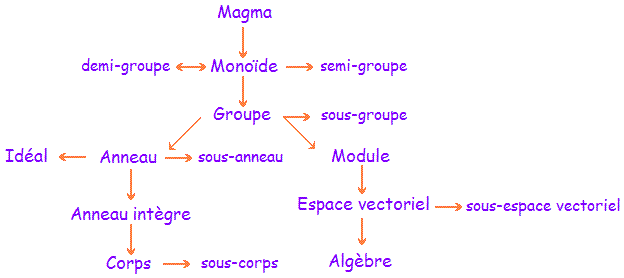
On s’est donc mis à enseigner la fameuse théorie des ensembles, les groupes, les corps, les anneaux… La réforme fut brutale et la résistance fut énorme.

Le cœur des résistants : « Comment ça, changer les mathématiques de nos pères ? Celles que l’on enseignait depuis la plus haute antiquité ? Avec ces ensembles nos enfants ne sauront plus compter. Les trains ne seront plus à l’heure, les robinets couleront sans arrêt dans la baignoire… »

On aurait pu appelé cette réforme, l'enseignement de...

l'algèbre générale, ou algèbre abstraite

C'est la branche des mathématiques qui porte principalement sur l'étude des structures algébriques et de leurs relations. L'algèbre générale possède beaucoup de connexions avec toutes les branches des mathématiques. C'est la mathématique.

Par exemple, la topologie algébrique utilise des objets algébriques pour son étude. La théorie algébrique des nombres étudie divers anneaux numériques qui généralisent l'ensemble des entiers. C’est en utilisant la théorie des nombres algébriques qu'Andrew Wiles a prouvé le dernier théorème de Fermat.

Un des grands mathématiciens qui s’illustra dans ce domaine au début dur XXième siècle est

une mathématicienne.

Emmy Noether (1882-1935).

Elle mérite une note à part. Demain peut-être.

* Si vous aimez un peu les maths, lisez le livre de Ian Stewart. Je n'ai pas fini mais j'avance doucement.

N. Bourbaki est-il vraiment mort ?

Le célèbre mathématicien né, en 1934, serait mort le 11 novembre 1968. 

C'est du moins ce que laissait entendre ce faire-part signé Jacques Roubaud:

Les famillesCantor, Hilbert, Noether,Les famillesCartan, Chevalley, Dieudonné, Weil,Les famillesBruhat, Dixmier, Godement, Samuel, Schwartz,Les famillesCartier, Grothendieck, Malgrange, Serre,Les famillesDemazure, Douady, Giraud, Verdier, Les famillesFiltrantes à droite et les épimorphismes stricts, Mesdemoiselles Adèle et Idèle,

ont la douleur de vous faire part du décès de M. Nicolas Bourbaki, leur père, frère, fils, petit-fils, arrière petit-fils et petit-cousin respectivement, pieusement décédé le 11 novembre 1968 (jour anniversaire de la victoire) en son domicile de Nancago.

L'inhumation aura lieu le samedi 23 novembre 1968 à 15h au cimetière de fonctions aléatoires, métros Markov et Gödel. On se réunira devant le bar « aux produits directs » carrefour des résolutions projectives, anciennement place Koszul. Selon le voeu du défunt une messe sera célébrée en l'église Notre-Dame-des-problèmes-universels par son éminence le cardinal Alephun, en présence de toutes les classes d'équivalences et des corps (algébriquement clos) constitués. Une minute de silence sera observée par les élèves des écoles normales supérieures et des classes de Chern, car « Dieu est le compactifié d'Alexandrov de l'univers » (Grothendieck, IV, 22).

Mais on sait qu'il faut se méfier des oulipiens et compte tenu des textes (posthumes dit-on?) signés N. Bourbaki publiés après 1968, on peut en douter. Comme pour assassinat de Kennedy, le mystère reste entier d'autant plus que l'on a toujours pas de démonstration de l'hypothèse de Riemann.

On vote aujourd'hui et il y a du vent. Pas d'excuse du genre "Il faisait trop beau, on est partis à la montagne et on a pas pu revenir avant 18 heures." pour ne pas voter. Non, les citoyens vont se précipiter en masse dans les bureaux de vote.

A St Julien, il y avait une queue pas possible sous la pluie, on attendait tranquillement notre tour avec le petit Clément, 4 ans, qui avait plein de pièces dans sa poche pour... payer les baguettes. On a pas acheté de mille-feuilles, juste deux baguettes.

Au bureau de vote en revanche, personne. Les trois préposés avaient l'air de s'ennuyer ferme. J'ai quand même mis un bulletin dans l'enveloppe et Clément à mis celle-ci dans l'urne. "A voter" a dit la dame. Voilà, c'est fait. On a remplacé les cantonales par des départementales. On a divisé par deux les cantons et multiplié par deux les candidats. Même les plus mauvais en math auront constaté 2/2 = 1. L'unité que l'on peut multiplier par n'importe quoi et qui donne toujours n'importe quoi. 

C'est ce qu'on appelle une grande réforme territoriale. La droite n'a pas changé le mille-feuille, la gauche non plus. On aura donc la même crème entre les couches du gâteau, des maires conseillers départementaux quand il ne sont pas conseillers régionaux ou députés-maire ou sénateurs-maire. Il y en a qui étaient déjà maires dans les années soixante-dix d'autres qui le seront encore en 2050. La démocratie prend encore un coup de jeune, elle ne survivra pas à tant de changements. Et Marine est en embuscade, elle attend la grande marée d'équinoxe.  

Un vague sentiment de perdre mon temps aujourd'hui... Mais Vialatte me rassure : 

Le temps perdu se rattrape toujours, et il ajoute,

peut-on rattraper celui que l'on a pas perdu ?

Vialatte a-t-il raison ?

C'est une question difficile. Le mathématicien anglais Penrose (1937-) répond à cette question en 1973, à propos d’un sujet de relativité générale : « On ne sait jamais vraiment quand on perd son temps » Conclusion: comment peut-on le rattraper ? 

Penrose a fait la découverte des ses fameux pavés en perdant son temps, il cherchait un jeu. Il a trouvé un pavage nouveau et non périodique. Quelques temps après,on découvre dans la nature des matériaux présentant une structure fortement ordonnée comme celle des cristaux mais non périodiques : les quasi-cristaux. Les pavages non périodiques de Penrose s'avèrent alors un modèle plausible de ces étranges matériaux.

Bon assez de théorie.

Pour les pavages périodiques, on a l'Alhambra,

ce magnifique palais de Grenade.

L'Alhambra ! L'Alhambra ! Palais que les génies

Ont doré comme un rêve et rempli d'harmonies,

Forteresse aux créneaux festonnés et croulants

Où l'on entend la nuit de magiques syllabes

Quand la lune, à travers les mille arceaux arabes,

Sème les murs de trèfle blanc.

                                                   Victor Hugo

Pour les pavages de Penrose, on a certaines œuvres de MC Escher. Ne pas confondre avec Stephan le chanteur qui d'ailleurs s'écrie Eicher. A noter que Maurits Cornelis Escher avait 33 ans de plus que Penrose, mais il avait l'esprit encore vif quand le mathématicien a trouvé ses pavés.

Penrose est aussi connu pour son triangle et ses escaliers qui ont beaucoup inspiré Escher :

Difficile d’ignorer Candy Crush, difficile de ne pas y jouer et encore plus difficile de ne pas tomber dans l’addiction. C’est un jeu de bonbons virtuels. Il semble bien que ce jeu séduise plus les femmes que les hommes. Téléchargeable gratuitement sur smartphones, tablettes et Facebook, Candy Crush était joué 700 millions de fois chaque jour dans le monde en décembre dernier.

Le problème semble simple, il suffit d’aligner le plus de bonbons par 3, 4 ou 5. Chaque mouvement change la configuration du jeu, il faut donc anticiper les alignements futurs et c’est ici que l’on tombe sur un sacré problème de math. Un chercheur australien a démontré que ce problème est de la classe des problèmes NP-complets donc très complexes.

Toby Walsh, le chercheur australien a étudié le jeu et découvert qu'il faisait partie d'une classe de problèmes mathématiques dits NP-difficiles et que si on ne limitait pas la taille du tableau de bonbons ce problème devient NP-complet.

Je n’entrerai pas ici dans l’explication sur les problèmes P et NP, disons que les NP-Complets sont des problèmes aux solutions difficiles à trouver mais faciles à prouver. On peut citer, le problème du voyageur de commerce, Les problèmes de coloration de graphe, le problème du sac à dos…

Walsh se demande s'il serait possible de tirer profit du temps que les gens passent à résoudre les problèmes de Candy Crush. Les adeptes cumulent plusieurs millions d'heures de jeu. Peut-être pourrait-on en profiter pour glisser quelques problèmes NP-difficiles concrets au milieu du jeu et ainsi faire avancer les mathématiques sur un des problèmes à 1 million de dollars.