13/12/2013
Spirale
 Stanisław Ulam est né à Lviv, aujourd’hui en Ukraine, en 1909. Il entra aux USA en 1938 comme boursier à Harvard. En 1943, son ami mathématicien John von Neumann l'invita à Los Alamos, où se construisait secrètement la bombe atomique. Joueur, il suggéra d'employer la méthode de Monte-Carlo pour évaluer les intégrales mathématiques difficiles qui apparaissent en modélisant les réactions nucléaires en chaîne.
Stanisław Ulam est né à Lviv, aujourd’hui en Ukraine, en 1909. Il entra aux USA en 1938 comme boursier à Harvard. En 1943, son ami mathématicien John von Neumann l'invita à Los Alamos, où se construisait secrètement la bombe atomique. Joueur, il suggéra d'employer la méthode de Monte-Carlo pour évaluer les intégrales mathématiques difficiles qui apparaissent en modélisant les réactions nucléaires en chaîne.
 Ulam montra que le précédent modèle de la bombe H était inexact. Il fut le premier à théoriser la bombe H allumée par une bombe A. Il travailla à la théorie des ensembles, la topologie, la théorie ergodique, et d'autres domaines des maths.
Ulam montra que le précédent modèle de la bombe H était inexact. Il fut le premier à théoriser la bombe H allumée par une bombe A. Il travailla à la théorie des ensembles, la topologie, la théorie ergodique, et d'autres domaines des maths.
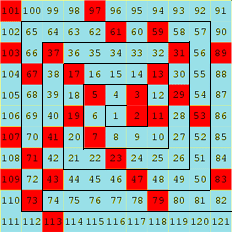
Un jour qu’il s’ennuyait grave lors d’un congrès de mathématiques, il commença sur un papier quadrillé à noter les nombres entiers en spirale. Et chose surprenante, les nombres premiers apparaissaient dans les diagonales. On retrouvait sur une diagonale les 40 nombres engendrés par le fameux polynôme d’Euler x² + x + 41... Mais finalement rien de bien nouveau.
Du coup, Ulam conscient que ses gribouillages n'aboutissaient pas à grand chose, abandonna ce sursaut de fantaisie et retourna donner des conférences sur la relation entre science et moralité, à la grande déception des amoureux de nombres premiers comme Paul Erdős.
Spirale 250 par 250

10:11 Publié dans Mathématique | Lien permanent | Commentaires (0) |
11/12/2013
Sobriété
Albert Cossery et Paul Erdös avait deux points en commun : Il sont nés il y a un siècle, en 1913, et ils ont tous deux vécu dans la plus grande sobriété.
 Albert Cossery est né au Caire dans un famille syro-libanaise d’origine grec. A 18 ans, il écrit en français « Les hommes oubliés de Dieu » qui sera publié par Henry Miller aux Etats-Unis. En plus de soixante ans d’écriture, il publie très peu de livres tous habités par d’êtres marginaux, voleurs ou fainéants philosophes qui cultivent l'humour comme la dérision.
Albert Cossery est né au Caire dans un famille syro-libanaise d’origine grec. A 18 ans, il écrit en français « Les hommes oubliés de Dieu » qui sera publié par Henry Miller aux Etats-Unis. En plus de soixante ans d’écriture, il publie très peu de livres tous habités par d’êtres marginaux, voleurs ou fainéants philosophes qui cultivent l'humour comme la dérision.
À la question : « Pourquoi écrivez-vous ? », Albert Cossery répond : « Pour que quelqu'un qui vient de me lire n'aille pas travailler le lendemain »… Il vivra 60 ans à Paris à l’hôtel Louisiane dans une pauvreté revendiquée et une joie de vivre chaque jour renouvelée. C’est là qu’il meure en 2008.
 Paul Erdös est né à Budapest, hongrois, d'origine juive, célèbre pour son excentricité, le nombre de ses publications scientifiques (environ 1 500) et de ses collaborateurs (plus de 500). La vie de Paul Erdős a été tout entière consacrée à ses travaux de recherche.
Paul Erdös est né à Budapest, hongrois, d'origine juive, célèbre pour son excentricité, le nombre de ses publications scientifiques (environ 1 500) et de ses collaborateurs (plus de 500). La vie de Paul Erdős a été tout entière consacrée à ses travaux de recherche.
Célibataire endurci, comme Cossery, vivant dans un grand dénuement, il possédait une vieille valise et un sac plastique orange de supermarché ; sa seule possession importante à ses yeux était son petit calepin.
Chercheur très prolifique, toutes disciplines confondues. Il touche à tout, théorie des graphes, théorie des nombres, combinatoire... et améliore sans cesse l'élégance de ses démonstrations.
Dans sa chambre, en plus de ses livres, Cossery était riche de ses idées et de ses relations dans le monde des lettres, JP Sartre, Albert Camus, Boris Vian, Henry Miller, les surréalistes, des peintres, Picasso, Cézanne, Man Ray… En plus de sa valise, Erdöss, quant à lui, était riche de ses solutions mathématiques et de ses collaborateurs, plus de 500 signeront au moins un papier avec lui.
 Ce sont les nombres 1 de Erdös, autre fantaisie mathématique…
Ce sont les nombres 1 de Erdös, autre fantaisie mathématique…
Citations de Paul Erdös:
Peut-être bien que Dieu ne joue pas au dés avec l'univers, mais bon sang, il y a quelque chose d'étrange avec les nombres premiers.
Il y a trois stades à quoi on reconnait qu'un mathématicien devient sénile. Le premier, il oublie son théorème, le second, il oublie de fermer sa braguette, le troisième, il oublie d'ouvrir sa braguette.
Le télévision a été inventée par les russes pour détruire l'éducation américaine.
21:26 Publié dans Lecture, Mathématique | Lien permanent | Commentaires (1) |
07/12/2013
Knuth
 Un terabyte vaut 1 million de megabytes. Dans mon premier job, en 1973, on avait un IBM 1130 qui disposait royalement de 2 mégabytes de disque. Avec ce bijou, on gérait une entreprise de 250 personnes, on faisait des planning PERT de 2000 tâches, on faisait des calculs de structure pour le barrage de la Grande Dixence, on a dessiné les profils en long et en travers plus les vues en perspective de l’autoroute de contournement de Genève, des calculs de caténaires... etc...
Un terabyte vaut 1 million de megabytes. Dans mon premier job, en 1973, on avait un IBM 1130 qui disposait royalement de 2 mégabytes de disque. Avec ce bijou, on gérait une entreprise de 250 personnes, on faisait des planning PERT de 2000 tâches, on faisait des calculs de structure pour le barrage de la Grande Dixence, on a dessiné les profils en long et en travers plus les vues en perspective de l’autoroute de contournement de Genève, des calculs de caténaires... etc...
En 1982 un PC d'IBM avait 5 megabytes de disque dur.
L’autre jour, on m’a proposé un ordinateur domestique à moins de 400 euros qui disposait d’un terabyte sur disque.
La loi de Moore avait prévu un facteur mille en 12 ou 13 ans, un facteur un million en 25 ans. On y est… Et c’est comme ça que les jeunes cons deviennent des vieux cons bien plus vite qu’avant. L’informatique satisfait donc le principe bouddhiste de l’impermanence. Avec un telle accélération des flows (flux en anglais), les flots risquent de nous noyer. A quelle bouée se raccrocher ? La bouée Knuth ?
Donald Knuth, américain né en 1938 est professeur émérite de « l'art de programmer » à Stanford University. Pionnier de l'algorithmique, il est l'auteur d'une centaine d'articles et d'une dizaine de livres sur l'algorithmique et les mathématiques discrètes. Les 3 premiers volumes de The Art of Computer Programming (TAOCP – l’art de programmer des ordinateurs) demeurent des ouvrages de référence. A lire en anglais, avec un bonne dose d'aspirine a chaque page.
Eh oui, la manière dont fonctionnent les ordinateurs est à peu près la même qu’au début. Ils déroulent toujours plus vite des algorithmes toujours les mêmes ou presque, et c’est ainsi que Don Knuth ne vieillit pas… ou presque.

J'aimerais voir des milliers de programmeurs libres de faire ce qui leur plaît. C'est ce qui fait vraiment avancer le domaine.
Knuth jouant de l'orgue, merci Aredius
18:29 Publié dans Mathématique, Science | Lien permanent | Commentaires (3) |
24/12/2012
Couples
 Mariage suite…
Mariage suite…
Savez-vous qu’il existe une méthode pour trouver des mariages stables. En informatique, on appelle cela un algorithme*. Une sorte de moulinette à problémes. Problèmes conjugaux en l'espèce :-)
Supposons qu’on ait un nombre identique d’hommes et de femmes ayant chacun leur préférences. C’est à dire que chaque individu de nos deux groupes classe les individus de sexe opposé dans un ordre précis (du plus moche, mal foutu(e) et fauché(e) au plus beau (belle), élégant(e) et riche). On supposera pour simplifier que l’on n’a pas d’homosexuels.
Il faut apparier les couples en sachant que la solution ne peut pas contenir deux couples qui préféreraient leur partenaire respectif. (ex: Monsieur Dupont préfère Madame Durand à Madame Dupont, et Madame Durand préfère Monsieur Dupont à Monsieur Durand).
Pas fastoche !
Eh bien, en 1962, David Gale et Lloyd Shapley (Nobel d’économie cette année) ont prouvé qu'il était toujours possible de résoudre le problème des mariages stables quel que soit le nombre de couple à marier. Passés à la moulinette de Gale et Shapley, tout le monde finit par être en couple et tous les mariages sont stables. Ceci dit, l’algorithme n’est pas très catholique car il va tester tous les couples possibles pour voir si ça marche. Un grand gang bang, seule solution semble-t-il pour garantir au final des couples stables.
Le mot algorithme (et aussi algèbre) vient du nom latinisé du mathématicien arabe Al-Khawarizmi, surnommé « le père de l'algèbre ».
Juliette Gréco présentée par Georges de Caunes, le papa d'Antoine...
10:10 Publié dans Au fil de la toile, Mathématique | Lien permanent | Commentaires (0) |
25/09/2012
Smith
 J’ai beau trituré mon numéro de téléphone dans tous les sens, je ne lui trouve pas des masses d’originalité. Sa décomposition en nombre premiers donne des 2, des 3, un 7, et même 103 et 4339. La somme des chiffres donne 36, ce qui ne correspond pas à la somme des chiffres de sa décomposition en nombre premiers.
J’ai beau trituré mon numéro de téléphone dans tous les sens, je ne lui trouve pas des masses d’originalité. Sa décomposition en nombre premiers donne des 2, des 3, un 7, et même 103 et 4339. La somme des chiffres donne 36, ce qui ne correspond pas à la somme des chiffres de sa décomposition en nombre premiers.
Vous vous dites « ça y est, cette fois, le père Joël, il décartonne ». Eh bien pas du tout. Je cherche la célébrité. Une célébrité même modeste, si j’ose cet oxymore. C’est ce qui est arrivé à Harold Smith (téléphone 4937775) qui a observé que son numéro, de téléphone donc, avait pour somme de ses chiffres 44, idem pour sa décomposition (essayez, vous verrez). Son Beauf, Albert Wilansky, fit connaître ces nombres sous le nom de nombres de Smith. La série commence par 4, 22, 27, 58, 85, 94, 121, 166, 202, 265, 274, 319, 346, 355, 378, 382, 391, 438, 454, 483, 517, 526, 535, 562, 576, 588, 627, 634, 636, 645, 648, 654, 663, 666…

J’ai un 666 dans mon numéro de portable. C’est paraît-il le numéro du diable dans l’apocalypse de Jean. Versets 167 et 18 : « C'est le moment d'avoir du discernement : celui qui a de l'intelligence, qu'il interprète le chiffre de la bête, car c'est un chiffre d'homme : et son chiffre est six cent soixante-six. »
A noter
- que 666 est la somme des nombres de 1 à 36
- que 36 est la somme des nombres de 1 à 8.
- que la somme des cubes de 1 à 36 est égale à 666 × 666.
- 36 au cube est 6 × 6 × 6 × 6 × 6 × 6.
- que (6 × 6 × 6) + (6 × 6 × 6) + (6 × 6 × 6) + (6 + 6 + 6) = 666 ;
- de plus, on peut remarquer, que la somme des carrés des nombres premiers jusqu'à 17 donne 666. Ainsi : 2² + 3² + 5² + 7² + 11² + 13² + 17² = 666.
- que donc 666 est le 34ième nombre de Smith (666=2 × 3 × 3 × 37)
- que Sin(666°) = Cos(6.6.6°) = - la moitié du nombre d’or.
OK, j’arête avec mes chiffres. Je reprends mes recherches solitaires sans être tout à fait sûr que, si je découvre quelque chose, mon beauf le fera savoir urbi et orbi au monde des mathématiciens ébahis.
Je suis sur la piste des repunits et des nombres palindromiques... Il me semble qu'ils se ressemblent mais shutttt.
13:26 Publié dans Mathématique | Lien permanent | Commentaires (3) |
19/02/2012
Maths encore

A la suite de ma visite à l’assemblée nationale, j’avais recherché les vidéos des auditions sur les mathématiques en France et dans les science. Pas de pot, la vidéo était déjà archivées.
Du coup, j’ai demandé qu’ils la remettent. Et bien la voilà : La vidéo "OPECST : réunion avec MM. Cédric Villani et Ngo Bao Chau, médaillés Fields et de M. Yves Meyer, prix Gauss" du 17/11/10 que vous avez demandée est maintenant disponible. Vous pouvez dès à présent cliquer sur le lien ci-dessous pour y accéder : Voir la vidéo.
En cherchant des infos sur Cédric Villani, j’ai constaté qu’il y avait un salle Fokko Du Cloux à l’université Claude Bernard – Lyon 1 ce qui n’est que justice. Et comme c’est dimanche voici quelques beaux zooms sur des fractales et/ou pour les musiciens un morceau de musique fractale.
Musique Alberto Posadas
Et pour finir un autre animal la chrysode:
15:12 Publié dans Mathématique | Lien permanent | Commentaires (0) |
11/02/2012
Déformatique
Dans le petit fascicule que m’a donné Claude Birraux, dont j’ai parlé hier, Yves Meyer, médaille Gauss, dit : Dans une école primaire de Nice, Gérard Berry dispense un enseignement expérimental : il apprend paradoxalement aux enfants la pensée informatique sans ordinateur, avec un très grand succès. Je renvoie la balle à Gérard Berry, que je vous suggère de convoquer ici pour qu’il vous fasse part de sa réflexion absolument prodigieuse sur ce sujet. Sur ce, Claudie Haigneré, première astronaute française et ex-ministre affirme : Les cours de désinformatique de Gérard Berry, devant le collège de pataphysique, sont tout à fait étonnants !
 Moi, toujours à l’affût dès qu’on parle de pataphysique, je me précipite sur l’homme et sur le mot. Le mot, comme je n’en doutais est "déformatique". Que dit Google ? Presque rien du mot. Pourtant, déformatique, ça sonne vachement prometteur comme mot valise. L’informatique qui forme et qui déforme, même sans ordinateur, tout un programme.
Moi, toujours à l’affût dès qu’on parle de pataphysique, je me précipite sur l’homme et sur le mot. Le mot, comme je n’en doutais est "déformatique". Que dit Google ? Presque rien du mot. Pourtant, déformatique, ça sonne vachement prometteur comme mot valise. L’informatique qui forme et qui déforme, même sans ordinateur, tout un programme.
On pense au robot à Ducros (le vulgarisateur scientifique d’Europe I), gros robot dont se moquait Boris Vian en 1953 dans un lettre à André Parinaud, grand arbitre des élégances littéraires au Figaro qui semblait inquiet à cause du robot… Une lettre écrite par Boris en tant que grand satrape du collège de pataphysique. Lisez l'extrait sur le site et la référence à Pic de la Mirandole, célèbre pantomathe.
Donc, rien ou presque sur le mot. Peu de chose sur l’homme, polytechnicien et informaticien qui semble être un bon vulgarisateur plutôt conventionnel (Le numérique c’est l’avenir… Ben oui !) du moins à première vue googlisante. Si vous avez des infos ou des désinfos, je suis preneur… Les commentaires sont faits pour ça.
18:16 Publié dans Mathématique, Science | Lien permanent | Commentaires (6) |



